排队理论 - 应用场景
TL;DR
排队无处不在
性能分析
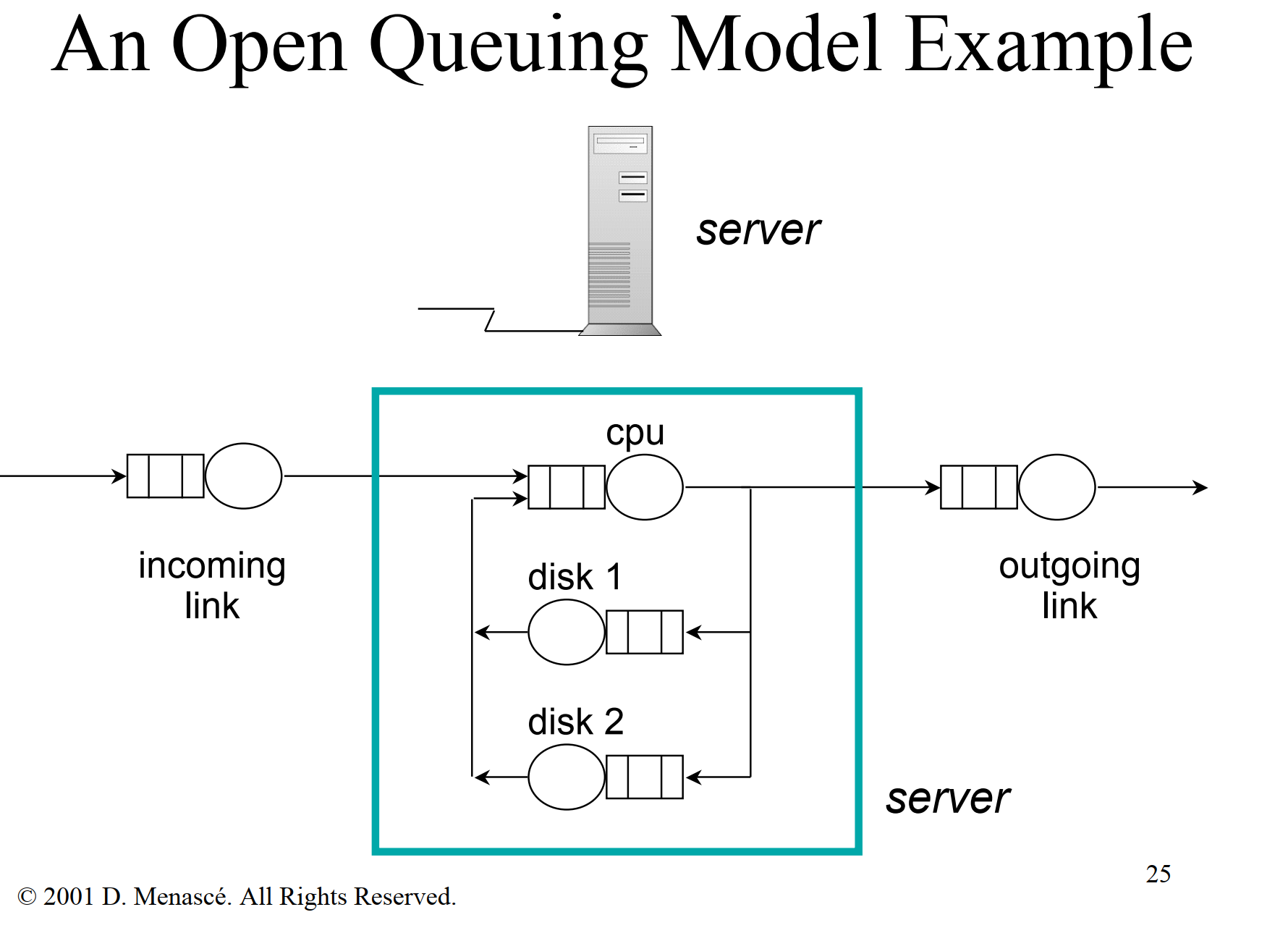
- V: average number of visits to queue i by a request
- S: average service time of a request at queue i per visit to the resource
- λ: average arrival rate of requests to queue i
- D: service demand of a request at queue i
- N: average number of requests at queue i, waiting or receiving service from the resource
- X: average throughput of queue i, i.e. average number of requests that complete from queue i per unit of time
- U the utilization :
Utilization Law
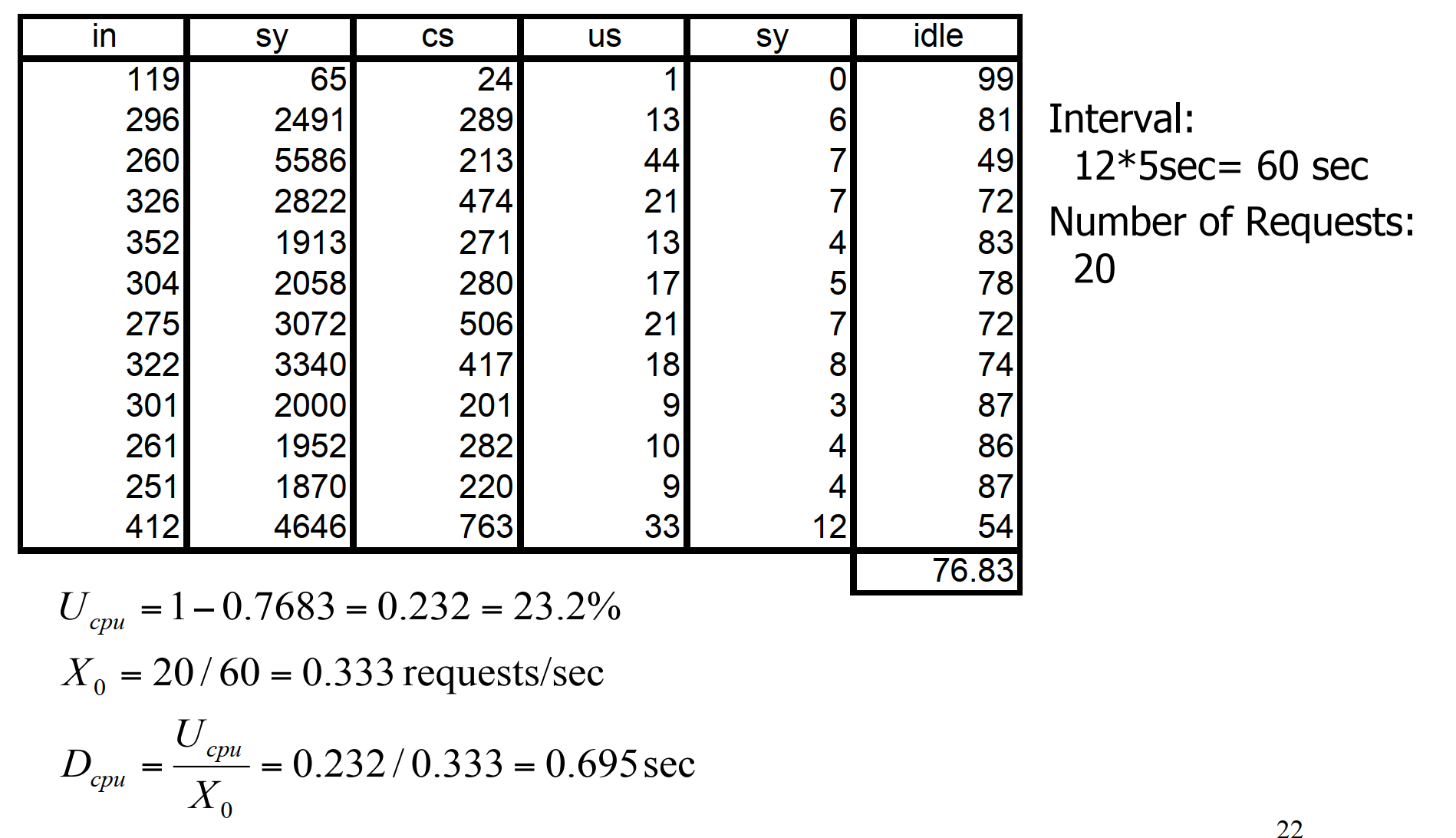
- iostat
[vagrant@centos8 ~]$ iostat -d -x 2
Linux 4.18.0-348.7.1.el8_5.x86_64 (centos8.localdomain) 02/28/2024 _x86_64_ (2 CPU)
Device r/s w/s rkB/s wkB/s rrqm/s wrqm/s %rrqm %wrqm r_await w_await aqu-sz rareq-sz wareq-sz svctm %util
sda 70.34 8.40 1896.11 374.21 0.51 4.36 0.72 34.19 1.12 1.68 0.09 26.96 44.55 1.05 8.25
dm-0 60.25 12.61 1836.02 381.57 0.00 0.00 0.00 0.00 0.95 1.77 0.08 30.48 30.25 0.72 5.25
dm-1 0.42 0.00 9.61 0.00 0.00 0.00 0.00 0.00 0.16 0.00 0.00 22.65 0.00 0.32 0.01
Device r/s w/s rkB/s wkB/s rrqm/s wrqm/s %rrqm %wrqm r_await w_await aqu-sz rareq-sz wareq-sz svctm %util
sda 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
dm-0 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
dm-1 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
Device r/s w/s rkB/s wkB/s rrqm/s wrqm/s %rrqm %wrqm r_await w_await aqu-sz rareq-sz wareq-sz svctm %util
sda 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
dm-0 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
dm-1 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
- Network utilization
一个网络段每秒传输1000个数据包,每个数据包的平均传输时间为0.15毫秒
Forced-Flow Law
定律 (FFL) 将系统内各个资源的吞吐量与整体资源的吞吐量联系起来
假设整个系统的到达速率为 V ,输出速率为 X ,第 k 个资源的输入速率为 Vk ,输出速率为 Xk
- 示例
数据库事务平均执行 4.5 个 I/O 数据库服务器上的操作。 一小时内 监控期间,执行了 7,200 笔交易
disk吞吐量时多少?
每笔I/O 处理耗时20毫秒,disk 利用率时多少?
求解:
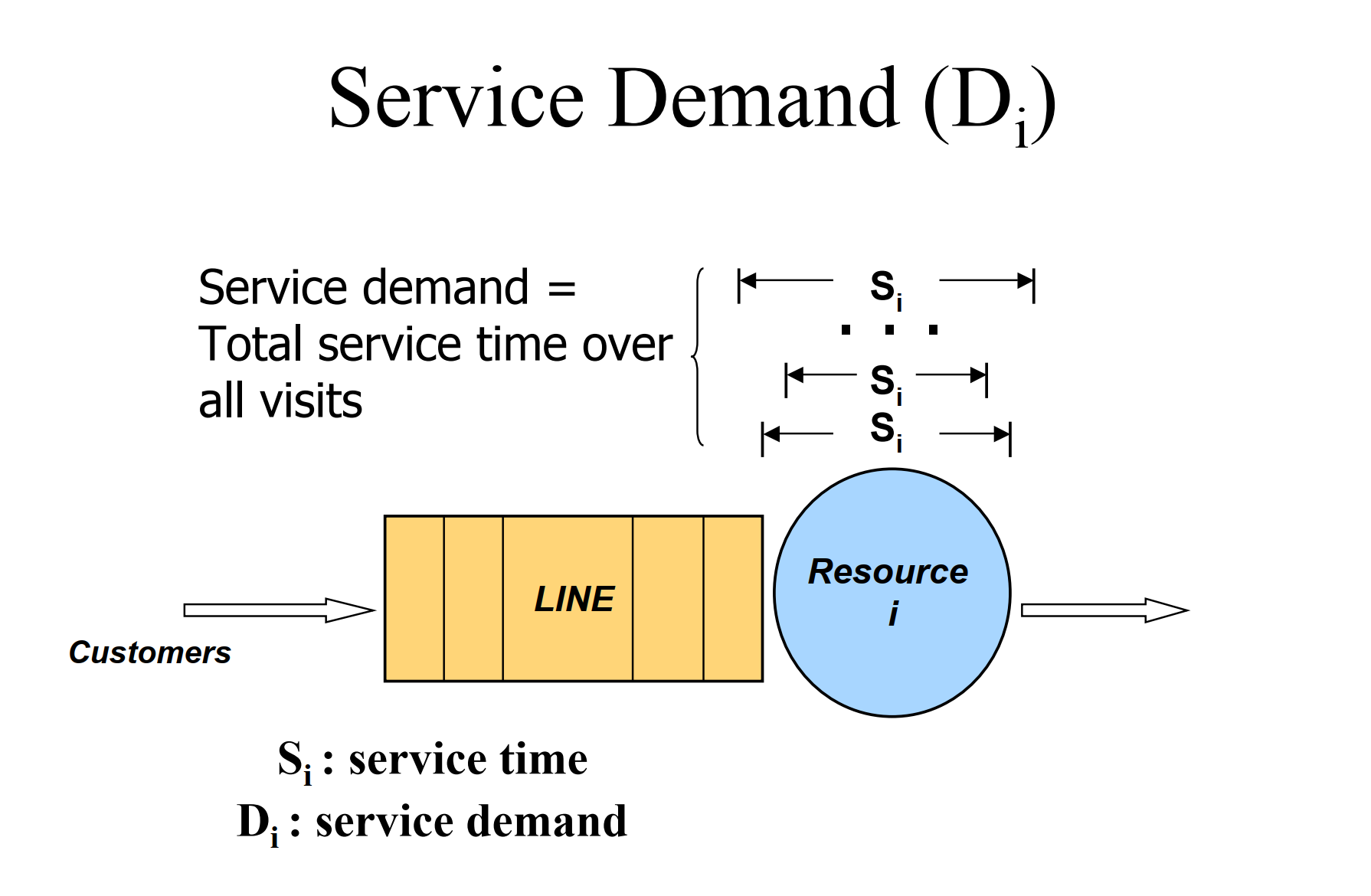
Service Demand Law
接上面,服务需求Di 与系统吞吐量有关
定义:服务需求定律表示利用率=服务需求x系统吞吐量。 由于平均服务时间为30ms,每笔交易访问磁盘3次,因此每笔交易需要的服务需求为3 x 30ms = 90ms。 一小时内,7200笔交易意味着吞吐量为7200/3600 = 2笔交易/秒
利用率0.09*2=0.18
- vmstat
容量规划
使用排队理论做容量规划
连接池(线程池同样适用)
Little’s Law 适用于任何处于稳定状态的排队系统 (到达率不大于出发率)
请求得到服务的平均时间仅取决于长期请求到达率和系统中的平均请求数
L = λ * W
- L - average number of requests in the system(包括正在处理和排队的)
- λ - long-term average arrival rate
- W - average time a request spends in a system
假设 程序级事务在其整个过程中使用相同的数据库连接,平均事务响应时间为100毫秒
W = 0.1 s
如果到达率 50/s
L = 50*0.1=5 connection requests
pool大小为 5 可以容纳平均传入流量,而无需将任何流量入队 连接请求。 如果池大小为 3,则平均有 2 个请求入队等待
Little’s Law适用于长期平均值,这可能不适合 考虑间歇性流量突发。 在现实场景中,连接池必须适应 短期流量高峰,因此考虑实际连接池吞吐量很重要
在排队论中,吞吐量用离开率(μ)来表示,对于连接池来说, 它表示给定时间单位内提供的连接数
以下练习演示了排队论如何帮助配置连接池 以支持各种传入流量峰值,复用👆的示例配置,测试的连接池边界如下
- 最多有 5 个正在服务的请求 (Ls),这意味着池最多可以提供 5 个 连接
- 平均事务响应时间为100毫秒
连接池每秒可以处理50个请求连接
当到达率等于出发率时,系统变得饱和,所有连接都处于状态使用
如果到达率超过连接池吞吐量,则溢出的请求必须等待连接变得可用
一秒突发 150 个请求的处理方式如下:
- 前 50 个请求可以在第一秒内得到满足
- 接下来的 100 个请求首先入队并在接下来的两秒内处理
Ls =5
Ws= 0.1
Lq = 10
Wq= 0.2
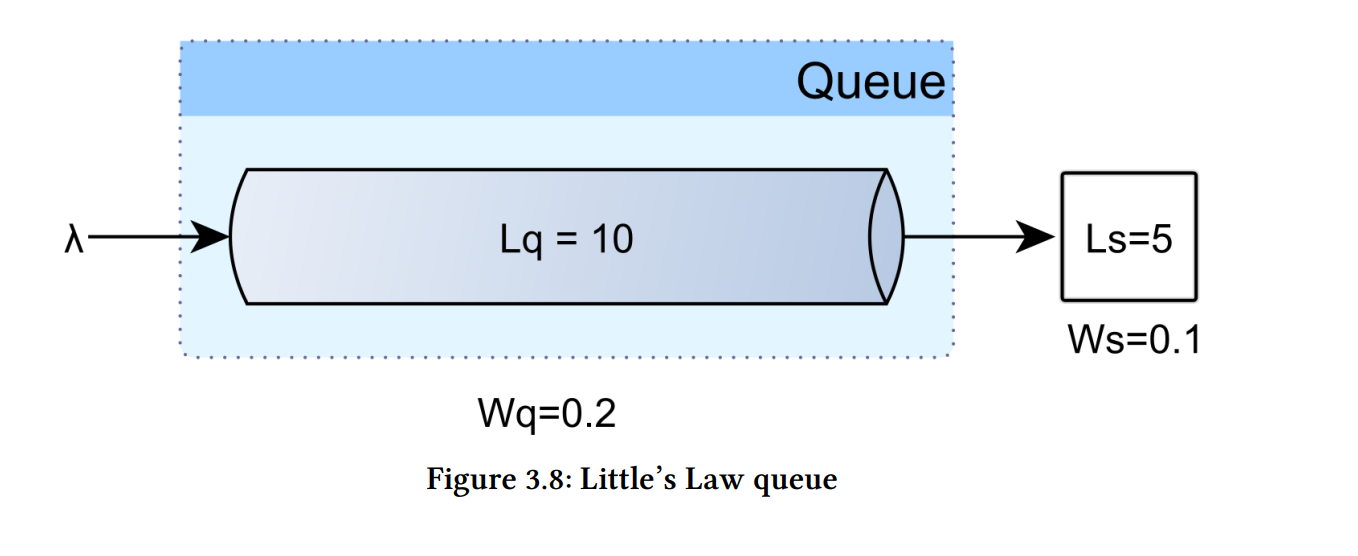
对于恒定的吞吐量,排队的连接请求数 (Lq) 与连接处理时间 (Wq)。 任何给定峰值中的请求总数计算如下:
排队的连接请求的数量和处理它们所需的时间如下:
假设 spike是250 r/s ,持续3s,最后请求再15s处理完毕
连接池此时size应该设置 λ = 700/14 = 50
系统容量规划
评估现有系统的容量是否合理?
-
监控线上的服务器是否存在利用率过低/过高的问题
-
OLTP
-
M/M/m模型,在保证响应时间的前提下,观察利用率与拐点的关系
-
监控各种资源的利用率,是否为Balanced Systems,是否有资源会最早达到瓶颈
- 所谓Balanced System,就是所有资源都有相同的利用率
- 混合系统-共享资源,计算复杂度增加
-
-
OLAP
- 可以使用较高的利用率,如果利用率不足,是否是任务调度不到位?优化调度算法
预估未来系统的容量?
- 预估系统Throughput
- 预估提供的Response Time
- 在系统压力极低的情况下,测试平均响应时间
R = W + S
什么是系统压力极地 , 等待时间 W->0 ,此时
- 根据以上得到的预估值,运用M/M/m模型,估算需要的Capacity - (上篇文章有公式)
- 这里计算的理论值,真实的环境比较复杂,不能直接用它来直接预测服务的负载、吞吐量、平均耗时等指标值
- 但是可以用来推断下理论值、极限值
性能优化
-
做高性能系统,在保证用户体验(Response Time)的同时,充分利用硬件资 源(Utilization),提供高吞吐率(Throughput),减少资源投入
-
与排队论需要解决的问题,达到了高度统一
-
排队论与Performance
- 响应时间 = 排队时间 + 服务时间 R = W + S
- 相同的硬件,系统提供高Throughput - > 更高的资源利用率 U
-
优化 Response Time
-
Profile 粒度越细,定位到的Performance瓶颈越准确
-
优化方法
-
Amdahl’s Law
- 系统整体可能的加速比受限于系统中的串行部分,在Java 中,减少锁的持有时间,减小锁的粒度,都能有效减少系统中的串行部分
- Response Time能够改进的程度,跟你改进模块在Response Time中所占的权重正相关,越耗时优化效果越明显
-
模块选择
- 根据Profile定位Response Time的分布
- 根据Amdahl’s Law,挑选潜在可优化的模块
- 根据难易程度,选择投入产出比最大的模块进行优化
-
-
优化实践 R = W + S
-
优化服务时间S
- 硬件/临界区
-
优化等待时间W
- 合并请求,减少一个业务操作访问server的次数
- 减少访问资源,如disck I/O次数、访问数据库次数
- 减少传输数据量,减少networking queue 等待
- ......
-
-
-
优化Throughput & Utilization
-
高吞吐率的背后,是各种资源的合理利用
-
Balanced System: cpu/memory / io 等
-
根据排队里论,资源利用率与响应时间有关系。在固定响应时 间下,不同的排队模型,能够达到的利用率是不同的
-
OLAP系统
- 对应于D/D/m模型,通过合理安排每个任务的调度,你可以获得极高的资源利用率
-
OLTP系统
- 对应于M/M/m模型,为了保证响应时间,必须将利用率限制在一定值之内
-
-
真实的场景下涉及到软硬件、网络、其他组件影响等等比较复杂的因素,用Little’s Law、Amdahl’s Law很难进行精准的分析,但是可以用来推断下理论值、极限值