聊聊 Queueing theory
定义
wiki定义: more
用于解决什么问题?
- 对服务provider来说:服务的利用率(成本)
- 对user来说:满足响应时间
总的来说,就是,再使用户满意的前提下,最大限度地控制成本,提高性价比
结合上面的问题,设置参数
什么时候过去,排队的时间会比较短?
- 单位时间平均到达请求数量:λ
不排队的话,需要多少时间?
- 单位时间平均完成的服务数量:μ
排队的话,前面还有几个再等待
- 平均队列长度 L
排队严重到什么程度,会放弃排队?
- 服务丢失率 Pb 排到我需要多少时间?
- Wait Time Wq
等我服务结束,又需要多少时间? Response Time R
多个队的话,哪个排队时间会看起来少? 队列利用率 U
这些参数后面会用到
Utilization Law
也称为稳态利用率公式(Steady-State Utilization Law)。这个定律描述了一个排队系统中,服务设备(例如服务器、服务窗口等)的利用率与系统中user到达率和服务率之间的关系
公式
其中:
- ρ:Server的利用率
- λ:单位时间内平均到达的顾客数(到达率)
- μ:单位时间内server能够完成的平均服务数(服务率)
总结
- 保持Server的服务速率不变,到达速率越高 -> Server利用率越高
- 保持到达速率不变, Server的服务速率越高 -> Server利用率越低;
Little’s Law
Little's Law 是一个用于排队系统的基本定律,它描述了系统中平均用户数(L)、平均到达率(λ)和平均逗留时间(W)之间的关系。具体而言,它表达了以下关系:
L = λW
其中这里:
- L 是系统中平均user数(也称为排队长度)
- λ 是平均到达率,表示每单位时间内到达系统的顾客数量
- W 是平均逗留时间,表示用在系统中逗留的平均时间
总结
- 平均响应时间越长W,队列长度也越长L
- 单位时间到达的请求越多λ,队列长度越长L
- 符合日常的理解
变种:Lq=λWq
Wq 排队等待时间
排队长度 = 到达率 * 平均等待时间
应用示例:
iostate
- avgrq-sz: 平均每次设备 I/O 操作的数据大小
avgrq-sz = (r/s+w/s)*await/1000
响应时间 VS 资源利用率 (R vs U)
S 表示服务时间
利用率U,服务时间S和响应时间R 之间关系
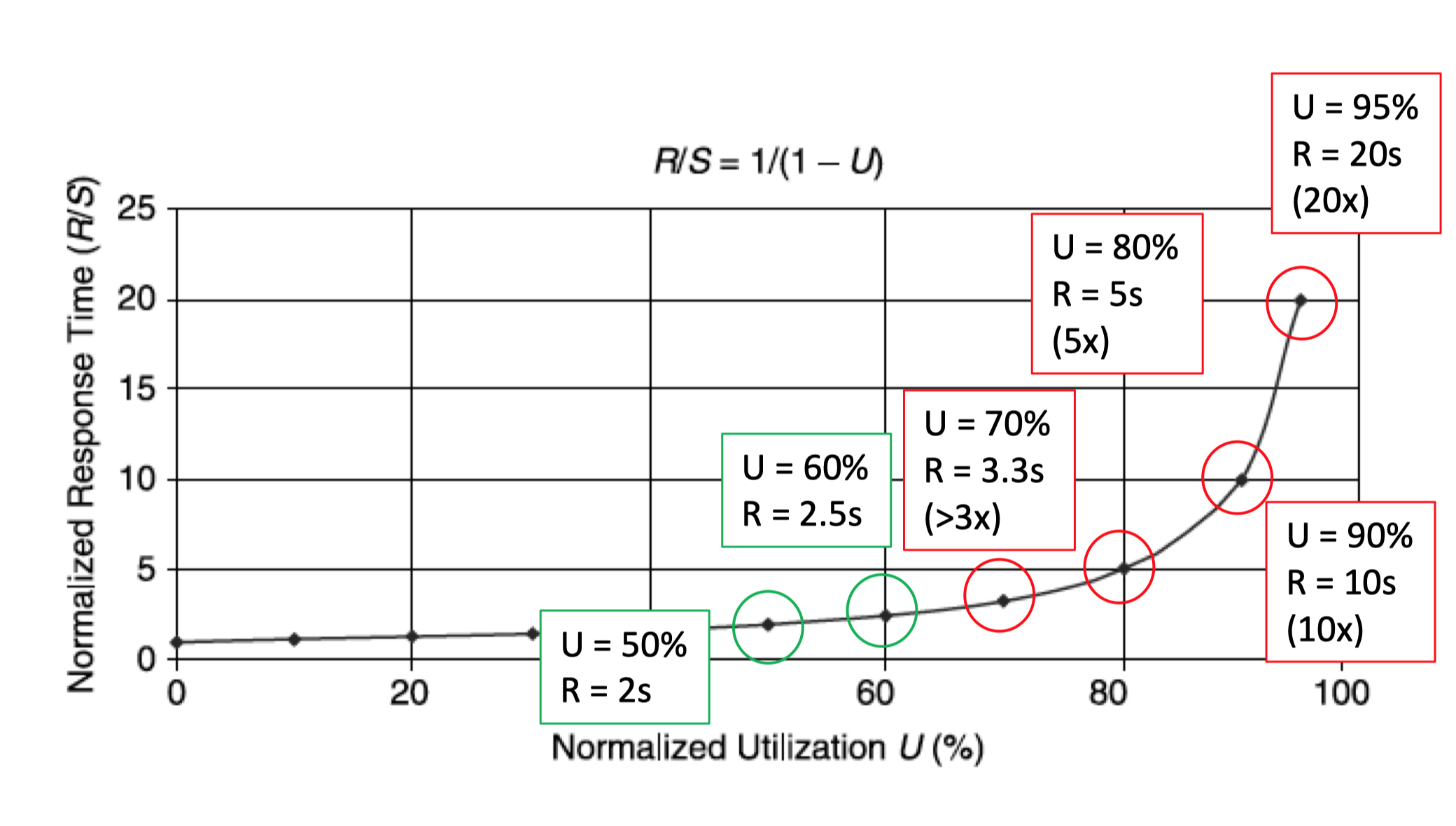
- 利用率增加 = 响应时间增加
- OLTP 系统的利用率应保持在70%以下
- 响应时间的增加不应超过服务时间的 3 倍
Kendall notation 肯德尔标记法
提供了一种简洁而标准的方式来描述排队系统的关键特征,使得人们能够更清晰地理解和比较不同排队系统的性能和行为
-
A 到达过程(Arrival Process):用字母表示,通常是 M/G/1(1表示1个server处理),其中:
- M 表示到达数量是泊松分布,到达事请求的时间间隔服从指数分布
- G 表示到达数量不具有任何单一概率分布的特点
- 其他常见的到达过程包括 D(确定性到达)
-
服务设备(Service Facility):用字母表示,通常是 M/M/1,其中:
- M 表示服务时间是指数分布,即user的服务时间服从指数分布。
- G 表示服务时间不具有任何单一概率分布的特点
- 其他常见的服务设备包括 D/D/1(确定性服务时间)、M/D/1(服务时间指数分布,到达时间确定)、M/G/1(服务时间指数分布,到达时间一般)等
-
排队规则(Queue Discipline):用字母表示,通常是 FIFO规则。其他常见的排队规则包括 LIFO、SIRO(服务设备上一次服务的顾客先被服务)、PS(优先级调度)
应用示例:
- 开放式排队系统(OLTP workloads)
M/M/1解读
到达请求的时间间隔指数分布/平均到达请求数量泊松分布 (M)
服务时间指数分布 (M)
一个Server (1)
无限等待队列长度 (默认)
无限请求数量 (默认)
FIFO调度策略 (默认)s
给定此模型,需要解决什么问题?
-
输入:已知
- 单位时间平均达到的请求数量 λ
- 单位时间平均处理能力 μ
-
输出
- server的利用率 U
- 平均服务时间 S
- 平均等待时间 W
- 平均响应时间 R
- 队列长度 Ls
- 等待队列长度 Lq
- 队列总长度 L
- server空闲率 Po
- 一个请求等待概率 Pb
到达速度大于处理速度,最终系统崩溃,反之,稳定状态
M/M/1 示例
- Server的利用率是多少?
- 平均服务时间是多少?
- 服务队列长度是多少?
- Server空闲概率是多少?
- 一个请求,需要等待的概率是多少?
- 队列总长度是多少?
- 等待队列长度是多少?
- 平均响应时间是多少?
- 平均等待时间是多少? W =R-S
利用率与响应时间之间的关系
OLTP应用模型
- 请求随机,服务时间随机
- 控制资源利用率
- 请求速度<处理速度 = 稳态系统
D/D/1
排队论中最简单的模型
- 到达请求的时间间隔分布:确定的
- 服务时间的分布:确定的
OLAP 应用模型
- 请求确定,服务时间确定,定时任务
利用率与响应时间之间的关系
- 可以人为调度各任务,做到完全的串行化
- 资源利用率可以达到100%,而不影响响应时间
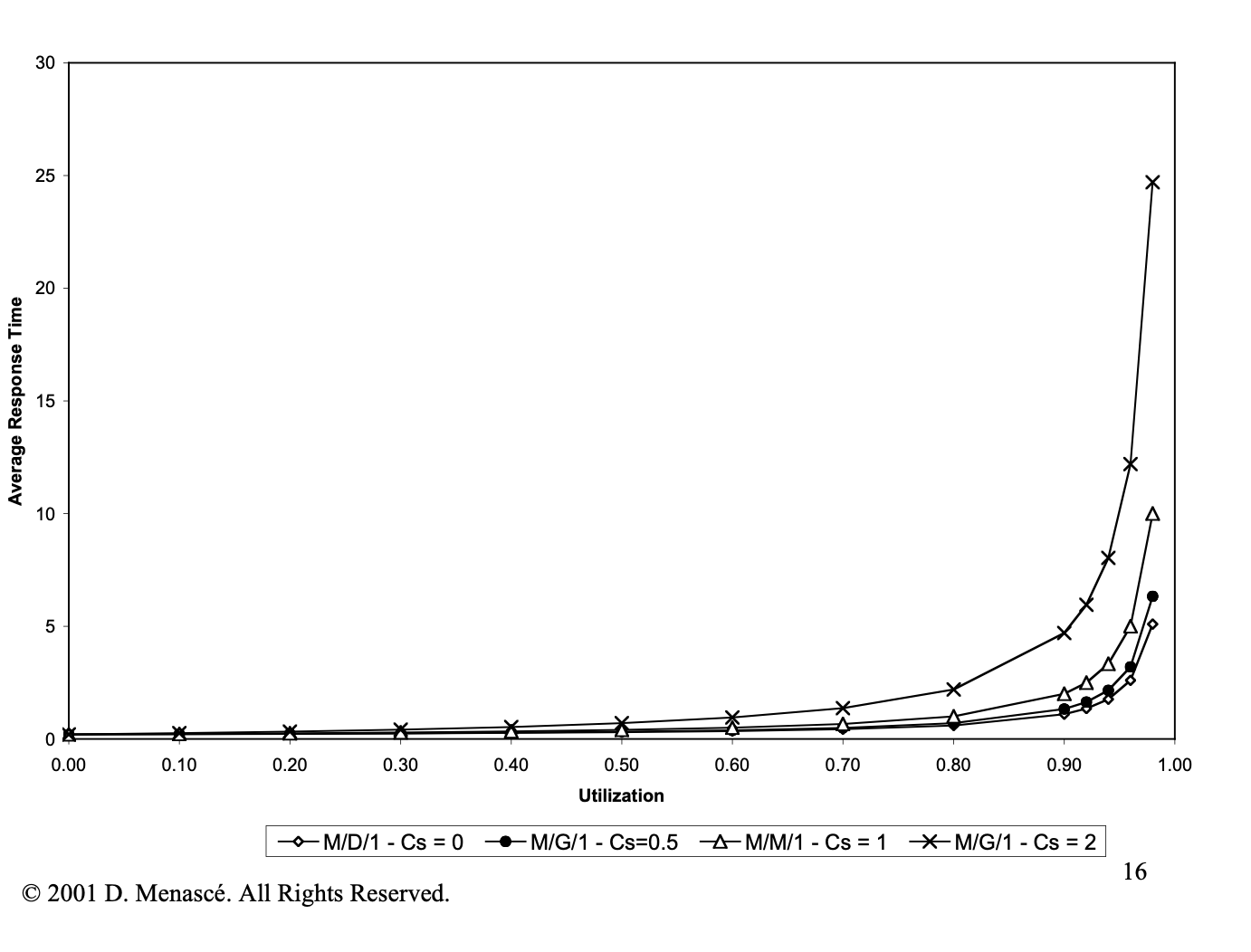
性能对比 M/M/1 vs M/D/1 vs M/G/1
M/M/1/N
相比M/M/1
- 等待队列数量有限 1个服务窗口, N-1个等待Buffers
- 若当前已有N个请求,则第N+1个请求被丢弃
- 大部分现实中的系统,都是有最大等待队列限制的
- 请求到达时,发现队列已满,而被丢弃的概率是多少?Pb
- M/M/1/N系统,不要求 < 1 ,因为超过系统限制的请求,都被 丢弃了
- M/M/1/N系统,实际进入系统的平均请求数量为λ=λ(1-Pb)
示例: ρ = 0.5 Pb = 0.001
n= 9
M/M/m
- m个Servers,一个排队队列(无限),每个Server的处理能力相同
- Server的利用率是多少?
- 响应时间
示例 λ =10 μ =1 求稳定太需要的m
性能对比
- m M/M/1 vs M/M/m
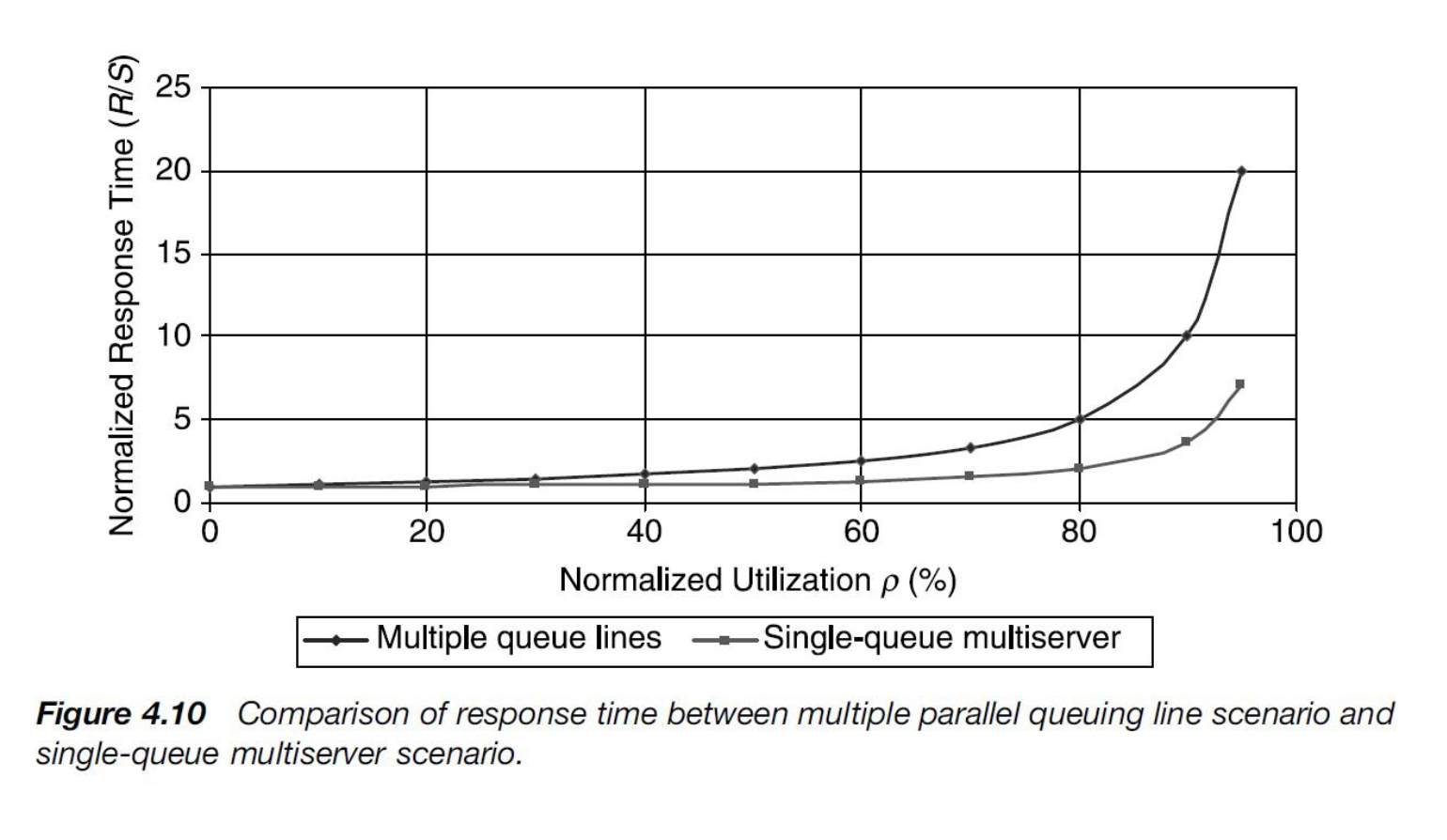
随着ρ增大,m M/M/1 的R增加更快
- M/M/m vs M/M/1
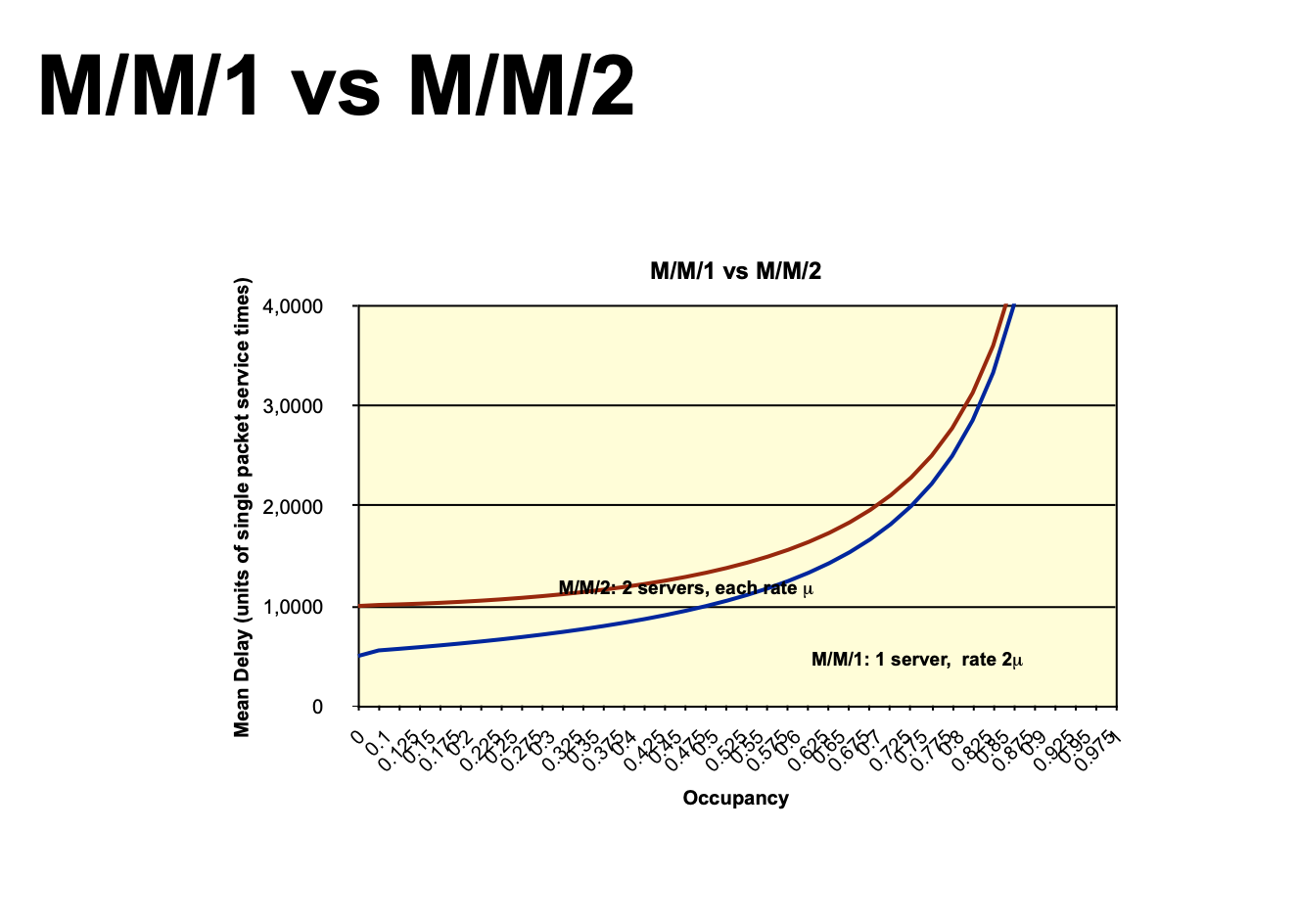
- M/M/1 优于M/M/m 优于 m M/M/1
- 银行排队,先领号之后等待叫号 -> M/M/m
- 硬件(如CPU)的发展,先追求的是极致的性能,当单Server到达瓶颈之后,才考虑向多 Servers发展
- 能将一个高性能Server资源使用到极致的系统,要优于堆积实例的系统:DB Server
参考
排队理论及其应用浅析 - 何登成